Linear Logic Game Diagram and Explanation

By popular demand, I am going to demonstrate below how to create a diagram for the Basic Linear LSAT Logic Game. 

We have 7 variables: ABCDEFG. (I wasn’t feeling creative that day.)

Here are the rules, numbered for quick reference:

1. Jandra must visit exactly two countries before her visit to China but after her visit to Bahrain.

2. China cannot be the last country she visits.

3. Jandra cannot visit Bahrain until she has visited Australia.

4. She cannot visit England immediately after she visits Djibouti, nor can she visit Djibouti immediately after she visits England.

5. Fiji must be visited either 4th or 5th.

***

 

The rules are not primarily about 1 variable going before or after another, as in a Pure Sequencing game. Instead, we have rules that refer to specific spaces, like rule 5, and other rules about immediacy/adjacency, like rule 4.

As such, I consider this game as a Basic Linear game and diagram it as such, with 7 spaces, numbered 1-7:

Rule 1 tells us we have 2 spaces between C and B. Those 2 are before C, and B’s even before those. As such, we’ll have B _ _ C . We can put a box around it to indicate that there are exactly 2 between them.

Rule 2 tells us C can’t be last, so we can place C with a slash through it under the 7th space.

Rule 3 tells us B can’t go before A goes. Because no 2 countries are visited simultaneously, we can say that A must go before B. We can diagram this as A – B. Since we already know that we have B _ _ C, we can combine the 2 rules to indicate that A is before B _ _ C, giving us:

Rule 4 tells us D and E can’t be adjacent (touching). As such, I’ll draw them touching in both orders and put a slash through each ordering. I’ll also put a box around them to indicate that their adjacency is what isn’t permitted.

Rule 5 tells us F must be 4th or 5th, so I’ll put F/ on 4 and /F on 5, to indicate that we either have F on 4 and something else on 5, or we have F on 5 and something else on 4.

I know that’s a lot to swallow, so here’s a diagram to clear things up for you:

 

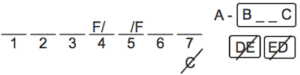
You could simply move on to the game’s questions at this point. However, I prefer to instead make some major inferences.

 

The B _ _ C rule is like the 800-pound gorilla taking up too many seats on the subway/bus/airplane/spaceship. By figuring out the limited places it can fit, we can make some major deductions about where everyone else goes.

B can’t start off on 1 because A’s got to go before it. B can’t end up on any of 5, 6, or 7 because we’ve got to fit “_ _ C” after it.

As such, B is limited to starting off this enormous unit on 2, 3, or 4, and we can create 3 separate stacked possibilities to represent those options. We can have B on 2 and C on 5, we can have B on 3 and C on 6, or we can have B on 4 and C on 7, generally speaking. Here’s what it initially looks like:

 

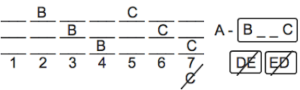
(I’ve temporarily removed Rule 5 – the one regarding F – from the image, but I’ll discuss it now.)

In the top possibility, because C’s on 5, we’ll need to have F on 4. We also know that A must be on 1 in order to go before B, due to Rule 3.

In the middle possibility, because neither B nor C is on either 4 or 5, F could be on either 4 or 5. We can now break this possibility in 2, based upon whether F goes on 4 or 5.

In the bottom possibility, F would have to be on 5, but this possibility is invalid because C can’t be on 7, due to Rule 2. As such, this option is eliminated.

So far, this might have been drawn as this:

However, I’ll now draw it as:

 

 

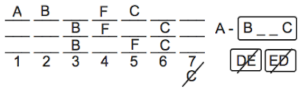
In the top possibility, we’ll need to have one of D or E go on 3 so that they’re not together on 6 and 7, which would violate Rule 4. The remaining spaces will feature G and whichever one of D or E didn’t go on 3. Either we’ll have G on 6 and one of the E/D pair on 7, or we’ll have G on 7 and one of the E/D pair on 6.

In each of the bottom 2 possibilities, A must be on either 1 or 2 to ensure that it goes before B, due to Rule 3. Because of this, we know that whatever happens, D and E will never be adjacent in either of these diagrams. That’s because 1 and 2 are the only remaining empty adjacent spaces in those diagrams.

 

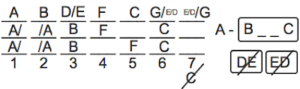
The top diagram is pretty much fleshed-out now. The bottom 2 diagrams lack only D, E, and G, which can go pretty much anywhere at this point, since we’re no longer in danger of having D and E be adjacent, and since G can always go anywhere.

As always, some of you will likely be thinking that this is way too much time invested up-front.

Is it possible to solve this game without a huge fancy diagram, simply using the basic diagram I drew earlier? Of course.

However, I’m all about showing you the deeper inferences so that you have a bird’s-eye view of the game whenever possible. This gives you a stronger jumping-off point from which to create hypothetical diagrams over the course of the game.

***

The text below contains the answers to the above Logic Game.

1. A

2. B

3. D

4. D

5. C