LSAT Logic Game Explanation | Grouping: Splitting

Here’s a complete explanation of the setup for the free LSAT Logic Game | Grouping: Splitting.

Take a look at the below explanation after trying that game.

Our variables are the 7 seagulls (ABCDEFG) grouped into two categories (male and female):

Male: ABCD

Female: EFG

The 7 seagulls are assigned to exactly one of two categories (Jacob and Hezekiah), making this a Grouping: Splitting game.

At least 2 males go to Jacob, and at least 2 females go to Hezekiah.

Simple enough.

Then we have the conditional rules:

1st conditional rule:

“If D shits on Jacob, then F does not shit on Hezekiah.”

D(J) -> NOT F(H)

However, since every seagull shits on exactly one of the two guys, if F doesn’t shit on Hezekiah, it must instead shit on Jacob.

Therefore, we can write the rule more simply as:

D(J) -> F(J)

We can also take the contrapositive:

NOT F(J) -> NOT D(J)

Again, this can be translated more simply as:

F(H) -> D(H)

Now we have the rule and its contrapositive:

D(J) -> F(J)

F(H) -> D(H)

2nd conditional rule:

“If D does not shit on Jacob, then G shits on Jacob.”

NOT D(J) -> G(J)

Again, because every seagull must shit on exactly one of the two guys, this is equivalent to:

D(H) -> G(J)

and the contrapositive – NOT G(J) -> NOT D(H) – becomes:

G(H) -> D(J)

So we now have:

D(H) -> G(J)

G(H) -> D(J)

We can link these rules together to form 2 conditional chains that are the contrapositives of each other:

Again, 1st conditional rule and its contrapositive:

D(J) -> F(J)

F(H) -> D(H)

2nd conditional rule and its contrapositive:

D(H) -> G(J)

G(H) -> D(J)

The rules containing D(H) can be linked to form a chain:

F(H) -> D(H) -> G(J)

The rules containing D(J) can be linked to form a chain:

G(H) -> D(J) -> F(J)

Final rule:“A and B will shit on the same man.”

We can simply represent this rule by stacking the variables vertically and placing a box around them.

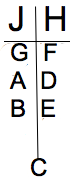
Here’s everything I’ve discussed up to this point:

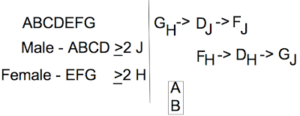
The “greater-than-or-equal to” signs on the left are just one way of representing the idea that at least 2 males go to J and at least 2 females go to H. You could also write down a range of 2-4 for males and 2-3 for females as an alternative.

You could also write down M and F instead of Male and Female to save space if you like. However, it might get confusing since there’s already a seagull with the variable F.

There’s still plenty to do here. At least 2 females go to H, but if you look at the two chains we have, they both end in a female going to J. Therefore, we can continue these chains by saying that if one female goes to J, the other two must go to H. On the top chain, if F goes to J, then E and G must go to H. On the bottom chain, if G goes to J, then E and F must go to H.

On the diagram, we now have the following:

 

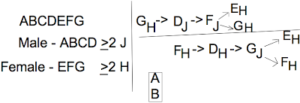
Admittedly, there’s a bit of recursion in the chain, but that’s okay.

(What I mean “recursion” is that the top chain starts and ends with G(H) and the bottom chain ends starts and ends with F(H).)

It’s just the nature of the game. For this reason, there’s not any benefit to taking the contrapositive of the new arrows just added (the ones regarding the females being at H) simply because it’ll further the recursiveness of the chains and give you nothing new.

However, one inference you can make from these two chains:

On the top chain, G(H) leads to E(H).

On the bottom chain, G(J) leads to (E)H.

This means that no matter where G occurs, E is always at H.

We can also arrive at this inference through a different method of reasoning:

Whenever G is at H, F is at J. Whenever F is at H, G is at J. Therefore, at least one of the two is always at J.

For this reason, we can’t ever have 3 females at H – in actuality, “at least 2 females at H” rule is “exactly 2.” Because we always need to have at least two females at H, E needs to be at H to give us a 2nd female there.

Breaking the Game Wide Open

Anyway, I use the F-G relationship discussed above to set up a few main diagrams that encompass all possibilities for the game. (The principle is that at least one must be assigned to a particular group.) Even if you don’t easily make the inference that E must go on H, you can still arrive at it naturally through the following technique.

Since at least one of F and G must go on J, we can set up 3 main diagrams that cover all possibilities. Either we have:

1. F on J and G on H

2. G on J and F on H

3. Both F and G on J

However, the 3rd possibility is impossible because then we would only have 1 female on H, but we are required to have at least 2 females on H.

Here are the 3 possibilities:

 

 

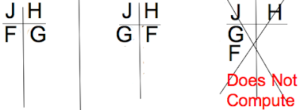
Now, in the 1st possibility, since F goes to J, E and G go to H. Since G is on H, D must go to J. (This is all using the conditional statements from earlier.) However, this does not determine where A and B go. We can have either both of A and B on J, or both of A and B on H. It looks like:

 

 

 

 

 

 

However, we still haven’t placed C.

In the top possibility, C can go on either side since the rules have now been satisfied and because there are no rules on the conditional chains that involve C.

In the bottom possibility, we already have two males on H. In order to meet the requirement that we have at least 2 males on J, C will have to go to J in that possibility, giving us:

 

 

 

 

 

 

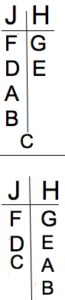
While the possibilities for F on J and G on H are now complete, this still leaves the possibility with G on J and F on H.

In that diagram, we can use the conditional rules to fill things in.

F on H requires D on H, and G on J requires E on H. Now, because we already have D on H, if we were to put the A-B pair on H, we wouldn’t be able to have at least 2 males on J – we could only have C on J, which wouldn’t be enough. Therefore, A and B must go to J. Now that we’ve satisfied the rules, C can go on either side.

 

 

 

 

So that’s the setup process, folks.

To put them all in one place, the main diagrams are the following (I’ve labeled them 1A, 1B, and 2 for your reference):

 

 

 

 

 

 

 

 

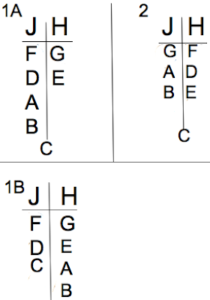
We can now see that there are only 5 valid scenarios for the game.

1A contains 2 scenarios, depending upon where C goes.

1B contains only 1 scenario because C’s placement is already determined.

2 contains 2 scenarios, depending upon where C goes.

***

With these 5 valid scenarios, you should be able to get through the game’s questions on your own. Most of the difficulty is in setting up the game, in making inferences from the rules, and listing the 5 scenarios as I’ve done above.