Several of you have rightfully hounded me for a complete seteup explanation for the free Advanced Linear Logic Game about monkeys in space, so here you go:
The description of the main diagram states:
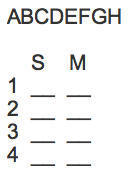
The seats are in consecutive rows that are numbered 1, 2, 3, and 4 from front to back. Each row contains exactly two seats: a seat with a window facing the sun and a seat with a window facing the moon.
Normally, I’d put the numbers 1, 2, 3, and 4 as the “base” (running horizontally). However, because the term “rows” typically describes sets of variables that are horizontal (as anyone who regularly uses Microsoft Excel can tell you), I’m going to make the numbers run vertically on the diagram.
The description gives us the following:
If you want to do make your numbers run horizontally that’s perfectly fine. You’ll just have to rotate everything 90 degrees as punishment for diagramming contrary to the way I do things.
Additionally, the placement of S on the left and M on the right is arbitrary.
Now, the rules, starting with the 1st rule:
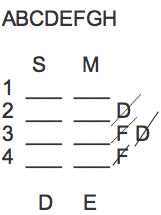
E’s window never faces the sun, but D’s window always faces the sun.
Since E doesn’t face the sun, it must face the moon. Put E below the moon column. Put D below the sun column.
The 2nd rule:
F sits in row 1 or row 2, but neither row 2 nor row 3 can contain D.
Place F with a slash through it next to rows 3 and 4, and D with a slash through it next to rows 2 and 3.
What you have should look something like this:
The next rule is a bit tricky to diagram:
B sits in the row immediately behind D’s row.
Thing is, they may not be in the same column (facing the same thing). 2 quick inferences we can make are that D’s not in row 4, and B’s not in row 1 (otherwise, how could B go behind D?). Since we already know D isn’t in rows 2 or 3, it must be in 1. Since B’s in the row immediately behind D’s, it must be in row 2.
Here’s one way you might want to diagram the rule itself (along with the new inferences included on the diagram):
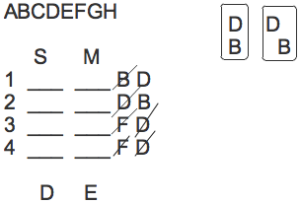
Of course we no longer need the indications of the rows that D and B aren’t going in, since we know exactly which rows they are going in. We now know that D must go in S1. I’ll erase the redundant information in the next pictured version of the diagram.
For now, the next rule:
If B’s window faces the sun, then A’s window faces the moon.
We can simply say, Bs -> Am.
The contrapositive would be:
If A’s window does not face the moon, then B’s window does not face the sun.
However, if A’s window is not facing the moon, we know it must be facing the sun. Similarly, if B’s window is not facing the sun, it must be facing the moon.
As such, rather than writing the contrapositive in negative terms, we can write it in positive ones:
If A’s window faces the sun, then B’s window faces the moon.
Diagrammed, this gives us: As -> Bm
We can simply write both of these conditional statements to the side of the diagram.
The next rule:
If D sits in row 1, then G sits in row 4.
Although this is a conditional statement, we already know through our inferences that D must, in fact, be in row 1. As such, since the sufficient condition of this rule must always be met, the necessary condition must always be met as well. We know with certainty that G must be on 4. Therefore, we should place G next to row 4.
We now have the following:
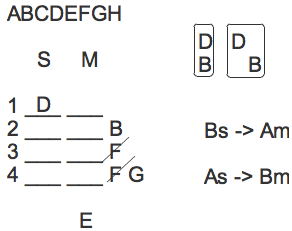
However, we can actually make two main diagrams, based upon whether B’s window faces the sun or moon:
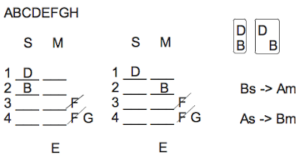
Now, when B faces the sun, we know A faces the moon, so we can go ahead and place A under the moon column in that particular diagram.
Now, the final rule:
If B sits in the same row as F, then G’s window faces the sun.
We already knew F couldn’t be in either of rows 3 or 4. Now, we also know that when it’s in row 2 (since B’s always in 2), we’ll get even more information.
We can diagram this rule as the following:

Every valid scenario must fall within 1 of these above 2 diagrams, and they’re more than enough to move on to the questions. By creating these up-front, you give yourself more of a starting point to draw hypothetical scenarios over the course of the game for particular questions. The game is too open-ended for you to draw every scenario up-front, but these diagrams will allow you to solve the questions more easily.
Most of you should simply move on to the questions with the diagrams that I’ve laid-out above. What we’ve done so far is enough to solve the questions without trouble.
However, if you’d like to see how it is possible to break the main diagrams apart even further (simply as an exercise), I’ll show those of you are interested how to do so, below.
***
You can split each of the 2 main diagrams above into 2 more (resulting in 4 main diagrams for all the non-math whizzes out there), based upon whether F goes to row 1 or row 2 in each of those diagrams.
On the left side, where B’s window faces the sun, I have F in row 1 in the top diagram and in row 2 in the bottom diagram.
On the right side, where B’s window faces the moon, I have F in row 1 in the top diagram and in row 2 in the bottom diagram.
Here’s what it looks like:
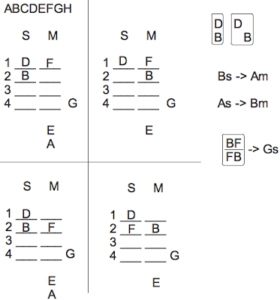
Now, in the bottom 2 diagrams, B and F are in the same row. As such, G’s window must face the sun in those diagrams. In the others, we simply don’t know whether G’s window faces the sun or the moon.
One more inference to make: the seat in the 3rd row facing the sun is particularly limited in the two diagrams on the left.
Since A’s window must face the moon in these diagrams, A can’t go there in these diagrams. Additionally, none of B, D, E, F, and G can go there – B, D, F have already been placed, G must go in row 4, and E’s window must always face the moon. As such, only either C or H can go in that seat on those diagrams. I’ll place C/H in the 3rd seat facing the sun on both of these diagrams:

Every valid scenario must fall within 1 of these 4 diagrams. By creating these up-front, you give yourself more of a starting point to draw hypothetical scenarios over the course of the game for particular questions.

